Introduction

The lsa.lin.reg function computes linear regression (Ordinary Least Squares, or shortly OLS) coefficients within groups of respondents defined by splitting variables. The splitting variables are optional. If no splitting variables are provided, the results will be computed on country level only. If splitting variables are provided, the data within each country will be split into groups by all splitting variables and the linear regression coefficients will be computed for the last splitting variable. Note that the linear regression coefficients can be computed with background/contextual variable as dependent, or PVs as dependent variables. Independent variables can be both background/contextual variables and sets of PVs. All analyses will take into account the complex sampling and assessment design of the study of interest. When sets of PVs are used either as dependent or independent variables, the regression coefficients will be computed between the background contextual variable and each PV in a set, and then the estimates for all PVs in the set will be averaged and their standard error computed using complex formulas which will depend on the study of interest. When sets of PVs are used both as dependent and independent variables, the first PV in the set for the dependent PVs will be regressed on the first PV in the set(s) of the independent one(s), then the second PV in the set of dependent PVs will be regressed on the second PV in the set(s) of independent ones, and so on. At the end, the estimates will be averaged and their standard error computed using complex formulas which will depend on the study of interest. Whatever the estimate is, the standard error will be computed taking into account the complex sampling and assessment designs of the studies. Refer here for a short overview on the complex sampling and assessment designs of large-scale assessments and surveys. If interested in more in-depth details on the complex sampling and assessment designs of a particular study and how estimates and their standard errors are computed, refer to its technical documentation and user guide.

Like any other function in the RALSA package, the lsa.lin.reg function can recognize the study data and apply the correct estimation techniques given the study sampling and assessment design implementation without extra care.

The linear regression function and its arguments

The lsa.lin.reg function has the following arguments:

data.file – The file containing lsa.data object. Either this or data.object shall be specified, but not both.
data.object – The object in the memory containing lsa.data object. Either this or data.file shall be specified, but not both.
split.vars – Categorical variable(s) to split the results by. If no split variables are provided, the results will be for the overall countries’ populations. If one or more variables are provided, the results will be split by all but the last variable and the percentages of respondents will be computed by the unique values of the last splitting variable.
bckg.dep.var – Name of a continuous background or contextual variable used as a dependent variable in the model.
PV.root.dep – The root name for a set of plausible values used as a dependent variable in the model.
bckg.indep.cont.vars – Names of continuous independent background or contextual variables used as predictors in the model.
bckg.indep.cat.vars – Names of categorical independent background or contextual variables used as predictors in the model to compute contrasts for (see bckg.cat.contrasts and bckg.ref.cats).
bckg.cat.contrasts – String vector with the same length as the length of bckg.indep.cat.vars specifying the type of contrasts to compute in case bckg.indep.cat.vars are provided.
bckg.ref.cats – Vector of integers with the same length as the length of bckg.indep.cat.vars and bckg.cat.contrasts specifying the reference categories for the contrasts to compute in case bckg.indep.cat.vars are provided.
PV.root.indep – The root names for a set of plausible values used as a independent variables in the model.
interactions – Interaction terms – a list containing vectors of length of two.
standardize – Shall the dependent and independent variables be standardized to produce beta coefficients? The default is FALSE.
weight.var – The name of the variable containing the weights. If no name of a weight variable is provide, the function will automatically select the default weight variable for the provided data, depending on the respondent type.
include.missing – Logical, shall the missing values of the splitting variables be included as categories to split by and all statistics produced for them? The default (FALSE) takes all cases on the splitting variables without missing values before computing any statistics.
shortcut – Logical, shall the “shortcut” method for IEA TIMSS, TIMSS Advanced, TIMSS Numeracy, PIRLS, ePIRLS, PIRLS Literacy and RLII be applied? The default (FALSE) applies the “full” design when computing the variance components and the standard errors of the estimates.
save.output – Logical, shall the output be saved in MS Excel file (default) or not
#’ (printed to the console or assigned to an object).
output.file – Full path to the output file including the file name. If omitted, a file with a default file name “Analysis.xlsx” will be written to the working directory (getwd()).
open.output – Logical, shall the output be open after it has been written? The default (TRUE) opens the output in the default spreadsheet program installed on the computer.

Notes:

Either data.file or data.object shall be provided as source of data. If both of them are provided, the function will stop with an error message.
The function computes linear regression coefficients by the categories of the splitting variables. The percentages of respondents in each group are computed within the groups specified by the last splitting variable. If no splitting variables are added, the results will be computed only by country.
If standardize = TRUE, the variables will be standardized before computing any statistics to provide beta regression coefficients.
Either a background/contextual variable (bckg.dep.var) or a root name of a set of plausible values (PV.root.dep) can be provided as dependent variable but not both.
Background/contextual variables passed to bckg.indep.cont.vars will be treated as numeric variables in the model. Variables with discrete number of categories (i.e. factors) passed to bckg.indep.cat.vars will be used to compute contrasts. In this case the type of contrast has to be passed to bckg.cat.contrasts and the number of the reference categories for each of the bckg.indep.cat.vars. The number of types of contrasts and the reference categories must be the same as the number of bckg.indep.cat.vars. The currently supported contrast coding schemes are:
1. dummy – the intercept is the average on the dependent variable for the respondents choosing the reference category and the slopes are the differences between intercept and the average of respondents on the dependent variable choosing every other category.
2. deviation – the intercept is the grand mean on the dependent variable regardless of the group and the slopes are the differences between intercept and the average of respondents on the dependent variable choosing every other category except the reference one.
3. simple – the same as for the dummy contrast coding, except for the intercept which in this case is the grand mean.
Note that when using standardize = TRUE, the contrast coding of bckg.indep.cat.vars is not standardized. Thus, the regression coefficients may not be comparable to other software solutions for analyzing large-scale assessment data which rely on, for example, SPSS or SAS where the contrast coding of categorical variables (e.g. dummy coding) takes place by default. However, the model statistics will be identical.
Multiple continuous or categorical background variables and/or sets of plausible values can be provided to compute regression coefficients for. Please note that in this case the results will slightly differ compared to using each pair of the same background continuous variables or PVs in separate analysis. This is because the cases with the missing values are removed in advance and the more variables are provided, the more cases are likely to be removed. That is, the function support only listwisie deletion.
Computation of regression coefficients involving plausible values requires providing a root of the plausible values names in PV.root.dep and/or PV.root.indep. All studies (except CivED, TEDS-M, SITES, TALIS and TALIS Starting Strong Survey) have a set of PVs per construct (e.g. in TIMSS five for overall mathematics, five for algebra, five for geometry, etc.). In some studies (say TIMSS and PIRLS) the names of the PVs in a set always start with character string and end with sequential number of the PV. For example, the names of the set of PVs for overall mathematics in TIMSS are BSMMAT01, BSMMAT02, BSMMAT03, BSMMAT04 and BSMMAT05. The root of the PVs for this set to be added to PV.root.dep or PV.root.indep will be “BSMMAT”. The function will automatically find all the variables in this set of PVs and include them in the analysis. In other studies like OECD PISA and IEA ICCS and ICILS the sequential number of each PV is included in the middle of the name. For example, in ICCS the names of the set of PVs are PV1CIV, PV2CIV, PV3CIV, PV4CIV and PV5CIV. The root PV name has to be specified in PV.root.dep or PV.root.indep as “PV#CIV”. More than one set of PVs can be added in PV.root.indep.
The function can also compute two-way interaction effects between independent variables by passing a list to the interactions argument. The list must contain vectors of length two and all variables in these vectors must also be passed as independent variables. Note the following:
1. When an interaction is between two independent background continuous variables (i.e. both are passed to bckg.indep.cont.vars), the interaction effect will be computed between them as they are.
2. When the interaction is between two categorical variables (i.e. both are passed to bckg.indep.cat.vars), the interaction effect will be computed between each possible pair of categories of the two variables, except for the reference categories.
3. When the interaction is between one continuous (i.e. passed to bckg.indep.cont.vars) and one categorical (i.e. passed to bckg.indep.cat.vars), the interaction effect will be computed between the continuous variable and each category of the categorical variable, except for the reference category.
4. When the interaction is between a continuous variable (i.e. passed to bckg.indep.cont.vars) and a set of PVs (i.e. passed to PV.root.indep), the interaction effect is computed between the continuous variable and each PV in the set and the results are aggregated.
5. When the interaction is between a categorical variable (i.e. passed to bckg.indep.cat.vars) and a set of PVs (i.e. passed to PV.root.indep), the interaction effect is computed between each category of the categorical variable (except the reference category) and each PV in the set. The results are aggregated for each of the categories of the categorical variables and the set of PVs.
6. When the interaction is between two sets of PVs (i.e. passed to PV.root.indep), the interaction effect is computed between the first PV in the first set and the first PV in the second set, the second PV in the first set and the second PV in the second set, and so on. The results are then aggregated.
Unless explicitly adding save.output = FALSE, the output will be written to MS Excel on the disk. Otherwise, the output will be printed to the console.
If no output file is specified, then the output will be saved with “Analysis.xlsx” file name under the working directory (can be obtained with getwd()).
If include.missing = FALSE (default), all cases with missing values on the splitting variables will be removed and only cases with valid values will be retained in the statistics. Note that the data from the studies can be exported in two different ways: (1) setting all user-defined missing values to NA; and (2) importing all user-defined missing values as valid ones and adding their codes in an additional attribute to each variable. If the include.missing is set to FALSE (default) and the data used is exported using option (2), the output will remove all values from the variable matching the values in its missings attribute. Otherwise, it will include them as valid values and compute statistics for them.
The shortcut argument is valid only for TIMSS, TIMSS Advanced, TIMSS Numeracy, PIRLS, ePIRLS, PIRLS Literacy and RLII. Previously, in computing the standard errors, these studies were using 75 replicates because one of the schools in the 75 JK zones had its weights doubled and the other one has been taken out. Since TIMSS 2015 and PIRLS 2016 the studies use 150 replicates and in each JK zone once a school has its weights doubled and once taken out, i.e. the computations are done twice for each zone. For more details see the technical documentation and user guides for TIMSS 2015, and PIRLS 2016. If replication of the tables and figures is needed, the shortcut argument has to be changed to TRUE.
The lsa.lin.reg also provides model Wald F-Statistic, as this is the appropriate statistic with complex sampling designs. See Bate (2004) and Rao & Scott (1984). The Wald F-Statistic is computed using Chi-square distribution and tests only the null hypothesis. The function provides two-tailed t-test and p-values for the regression coefficients.

The output produced by the function is stored in MS Excel workbook. The workbook has three sheets. The first one (“Estimates)” will have the following columns, depending on what kind of variables were included in the analysis:

<Country ID> – a column containing the names of the countries in the file for which statistics are computed. The exact column header will depend on the country identifier used in the particular study.
<Split variable 1>, <Split variable 2>… – columns containing the categories by which the statistics were split by. The exact names will depend on the variables in split.vars.
n_Cases – the number of cases in the sample used to compute the statistics.
Sum_<Weight variable> – the estimated population number of elements per group after applying the weights. The actual name of the weight variable will depend on the weight variable used in the analysis.
Sum_<Weight variable>_SE – the standard error of the the estimated population number of elements per group. The actual name of the weight variable will depend on the weight variable used in the analysis.
Percentages_<Last split variable> – the percentages of respondents (population estimates) per groups defined by the splitting variables in split.vars. The percentages will be for the last splitting variable which defines the final groups.
Percentages_<Last split variable>_SE – the standard errors of the percentages from above.
Variable – the variable names (background/contextual or PV root names, or contrast coded variable names). Note that when interaction terms are included, the cells with the interactions in the Variables column will contain the names of the two variables in each of the interaction terms, divided by colon, e.g. ASBGSSB:ASBGHRL.
Coefficients – the regression coefficients (intercept and slopes).
Coefficients_SE – the standard error of the regression coefficients (intercepts and slopes) for each independent variable (background/contextual or PV root names, or contrast coded variable names) in the model.
Coefficients_SVR – the sampling variance component for the regression coefficients if root PVs are specified either as dependent or independent variables.
Coefficients_<root PV>_MVR – the measurement variance component for the regression coefficients if root PVs are specified either as dependent or independent variables.
t_value – the t-test value for the regression coefficients.
p_value – the p-value for the regression coefficients.

The second sheet (“Model statistics”) contains the statistics related to the linear regression model itself in the following columns:

<Country ID> – a column containing the names of the countries in the file for which statistics are computed. The exact column header will depend on the country identifier used in the particular study.
<Split variable 1>, <Split variable 2>… – columns containing the categories by which the statistics were split by. The exact names will depend on the variables in split.vars.
Statistic – a column containing the R-Squared, adjusted R-Squared, Wald F-Statistic and degrees of freedom estimates.
Estimate – the numerical estimates for each of the above.
Estimate_SE – the standard errors of the estimates from above.
Estimate_SVR – the sampling variance component if PVs were included in the model.
Estimate_MVR – the measurement variance component if PVs were included in the model.
t_value – the t-test value for the regression coefficients, value only for the Wald F-Statistic is provided.
p_value – the p-value for the regression coefficients, value only for the Wald F-Statistic is provided.

The third sheet (“Analysis information”) contains some additional information related to the analysis per country in the following columns:

DATA – used data.file or data.object.
STUDY – which study the data comes from.
CYCLE – which cycle of the study the data comes from.
WEIGHT – which weight variable was used.
DESIGN – which resampling technique was used (JRR or BRR).
SHORTCUT – logical, whether the shortcut method was used.
NREPS – how many replication weights were used.
ANALYSIS_DATE – on which date the analysis was performed.
START_TIME – at what time the analysis started.
END_TIME – at what time the analysis finished.
DURATION – how long the analysis took in hours, minutes, seconds and milliseconds.

The fourth sheet (“Calling syntax”) contains the call to the function with values for all parameters as it was executed. This is useful if the analysis needs to be replicated later.

Computing linear regression coefficients using the command line

In the examples that follow we will merge a new data file (see how to merge files here) with student and school principal data from PIRLS 2016 (Australia and Slovenia), taking all variables from both file types:

lsa.merge.data(inp.folder = "C:/temp",
               file.types = list(acg = NULL, asg = NULL),
               ISO = c("aus", "svn"),
               out.file = "C:/temp/merged/PIRLS_2016_ACG_ASG_merged.RData")

lsa.lin.reg(data.file = "C:/temp/merged/PIRLS_2016_ACG_ASG_merged.RData",
            PV.root.dep = "ASRREA",
            bckg.indep.cont.vars = c("ASBGSSB", "ASBGSB"))

Few things to note:

The function can take one background/contextual variable or a set of PVs as dependent variable. The independent variables can be multiple background/contextual variables and/or sets of PVs.
The five PVs for the overall reading achievement are ASRREA01, ASRREA02, ASRREA03, ASRREA04, and ASRREA05. In the PV.root.corr argument we need to specify only the root of the PVs, “ASRREA”. The function will use this root/common name to select all five PVs and include them in the computations. For more details on the PV roots (also for the PV roots for studies other than TIMSS and PIRLS and their additions), the computational routines involving PVS, see here.
In international large-scale assessments all analyses must be done separately by country. There is no need, however, to add the country ID variable (IDCNTRY, or CNT in PISA) as a splitting variable. The function will identify it automatically and add it to the the vector of split.vars.
There is no need to specify the weight variable explicitly. If no weight variable is specified explicitly, then the default weight (total student weight in this case) will be used for the data set depending on the merged respondents’ data, it is identified automatically. If you have a good reason to change the weight variable, you can do so by adding the weight.var = "SENWGT", for example.
If no output file is specified, then the output will be saved with “Analysis.xlsx” file name under the working directory (can be obtained with getwd()).
Unless explicitly adding open.output = FALSE, to the calling syntax, the output file will be opened after all computations are finished. This is useful when multiple calling syntaxes for different analyses are executed and no immediate inspection of the output is needed.

Executing the code from above will print the following output in the RStudio console:

When all operations are finished the output will be written on the disk as MS Excel workbook. If open.output = TRUE (default), the file will be open in the default spreadsheet program (usually MS Excel). Refer to the explanations on the structure of the workbook, its sheets and the columns here.

Categorical variables can be added as contrast coded variables and the significance of the differences between the categories in the dependent variable (background/context or PVs) can be tested. For now, the function can work with the following contrast schemes: dummy, deviation, and simple (see here for description). Let’s test the differences in overall student reading achievement for those having different number of books at home (ASBG04) after controlling for how much students like reading scale (ASBGSLR, check the PIRLS 2016 technical documentation on how this scale is constructed and its properties). The number of books at home variables (ASBG04) has the following valid values:

None or very few (0-10 books)
Enough to fill one shelf (11-25 books)
Enough to fill one bookcase (26-100 books)
Enough to fill two bookcases (101-200 books)
Enough to fill three or more bookcases (more than 200)

We need to add ASBG04 as value of the bckg.indep.cat.vars argument of the lsa.lin.reg function. The function will automatically determine the valid values, but we need to specify the reference category as a values of the bckg.cat.contrasts (the type of contrast coding) and the bckg.ref.cat (the reference category). If we omit specifying a value for bckg.cat.contrasts (which we will), the function will automatically compute the regression coefficients with dummy coding (the intercept will be the average overall reading achievement for students who have chosen the category we set as a reference, see further) and the regression coefficients for the rest of the categories will be the differences in achievement for the students who chose any other category, but the reference. If any other contrast scheme is needed, it has to be specified explicitly, using the bckg.cat.contrasts argument, see here. We will define the first category (“None or very few (0-10 books)” at home). We will add how much students like reading scale (ASBGSLR, check the PIRLS 2016 technical documentation on how this scale is constructed and its properties) as a control variable as a value of bckg.indep.cont.vars. The calling syntax looks like this:

lsa.lin.reg(data.file = "C:/temp/merged/PIRLS_2016_ACG_ASG_merged.RData",
            PV.root.dep = "ASRREA", bckg.indep.cat.vars = "ASBG04",
            bckg.ref.cats = 1, bckg.indep.cont.vars = "ASBGSLR")

Executing the syntax from above will overwrite the previous output because it has the same file name defined (a warning will be displayed in the console). The columns in the “Estimates” sheet will now be different. For the meaning of the column names, refer to the list here.

Computing linear regression coefficients using the GUI

To start the RALSA user interface, execute the following command in RStudio:

ralsaGUI()

For the examples that follow, merge a new file with PIRLS 2016 data for Australia and Slovenia (Slovenia, not Slovakia) taking all student and school principal variables. See how to merge data files here. You can name the merged file PIRLS_2016_ACG_ASG_merged.RData.

When done merging the data, select Analysis types > Linear regression from the menu on the left. When navigated to the Linear regression in the GUI, click on the Choose data file button. Navigate to the folder containing the merged PIRLS_2016_ACG_ASG_merged.RData file, select it and click the Select button.

Once the file is loaded, you will see a panel on the left (available variables) and set of panels on the right where variables from the list of available ones can be added. Above the panels you will also see information about the loaded file.

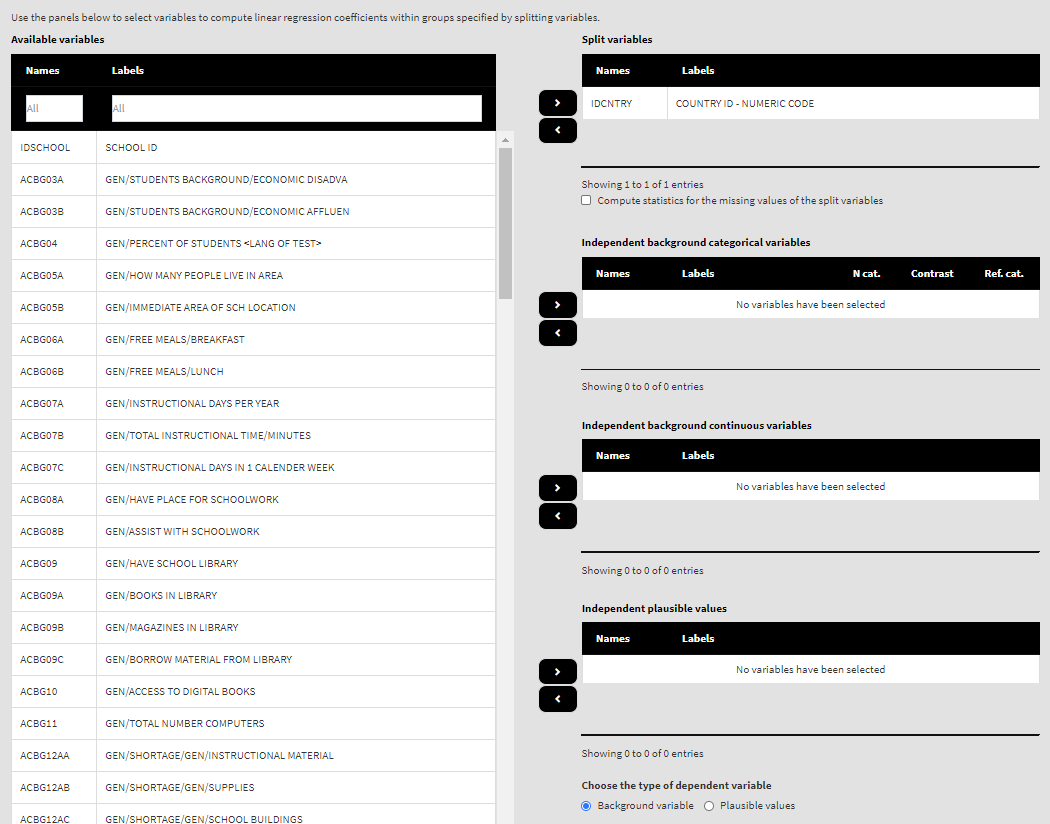
Use the mouse to select variables from the list of Available variables and the arrow buttons in the middle of the screen to add them to different fields (or remove them) to make the settings for the analysis. You can use the filter boxes on the top of the panels to find the needed variables quickly.

As a start, let’s compute the linear regression coefficients for a model where the dependent variable is the set of PVs for overall reading achievement, and the independent variables are two background scales – Students’ Sense of School Belonging (ASBGSSB) and Students Being Bullied (ASBGSB) in Australia and Slovenia (check the PIRLS 2016 technical documentation on how these scales are constructed and their properties). Select variables ASBGSSB and ASBGSB from the list of the Available variables and move them to the list of Independent background continuous variables using the right arrow button. Scroll down and from the pair of radiobutons under Choose the type of dependent variable select Plausible values. From the list of Available variables locate the root of the overall reading plausible values (ASRREA). You can use the filter boxes at the top of the panel to search for it, either by name or label. Select the root and add it to the Dependent plausible values panel using the right arrow button. This is all that needs to be done. Scroll down and click on the Define output file name. Navigate to the folder C:/temp/Results (or to the folder where you want to save the output) and define the output file name. After you do so, a checkbox will appear next to the Define the output file name. If ticked, the output will open after all computations are finished. Underneath you will see the Standardized coefficients checkbox. If ticked, the variables will be standardized before the statistics is computed. See here for more details. Underneath the calling syntax will be displayed. Under all of these the Execute syntax button will be displayed. The final settings in the lower part of the screen should look like this:

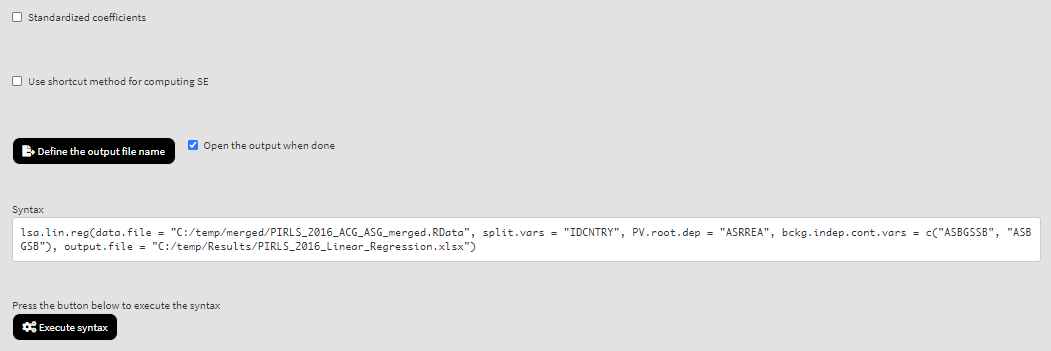
Click on the Execute syntax button. The GUI console will appear at the bottom and will log all completed operations:

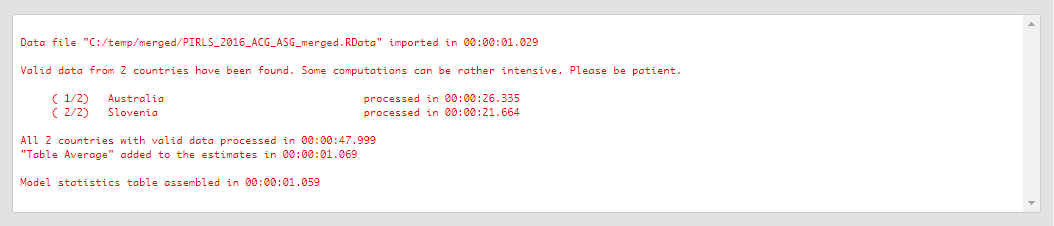
Few things to note:

The function can take one background/contextual variable or a set of PVs as dependent variable. The independent variables can be multiple background/contextual variables and/or sets of PVs.
The five PVs for the overall reading achievement are ASRREA01, ASRREA02, ASRREA03, ASRREA04, and ASRREA05. The lists of Available variables and Dependent Plausible values will not show the five separate PVs, but just their root/common name – ASRREA, without the numbers at the end. In the background, the function will take all the five PVs and include them in the computations. For more details on the PV roots (also for the PV roots for studies other than TIMSS and PIRLS and their additions), the computational routines involving PVS, see here.
In international large-scale assessments all analyses must be done separately by country. The country ID variable (IDCNTRY, or CNT in PISA) is always selected as the first splitting variable and cannot be removed from the Split variables panel.
The default weight variable is selected and added automatically in the Weight variable panel. It can be changed with another weight variable available in the data set. If the default weight variable is selected, it will not be shown in the syntax window. If no weight variable is selected in the Weight variable panel, the default one will be used automatically.
If the Standardized coefficients checkbox is ticked, the regression coefficients will be computed on standardized variables and beta coefficients will be included in the output.
The Use shortcut method for computing SE checkbox is not ticked by default. This will make the function to compute the standard error using the “full” method for the sampling variance component. For more details see here and here.

If the Open the output when done checkbox is ticked, the output will open automatically in the default spreadsheet program (usually MS Excel) when all computations are completed. Refer to the explanations on the structure of the workbook, its sheets and the columns here.

Categorical variables can be added as contrast coded variables and the signifficance of the differences between the categories in the dependent variable (background/context or PVs) can be tested. For now, the function can work with the following contrast schemes: dummy, deviation, and simple (see here for description). Let’s test the differences in overall student reading achievement for those having different number of books at home (ASBG04) after controlling for how much students like reading scale (ASBGSLR, check the PIRLS 2016 technical documentation on how this scale is constructed and its properties). The number of books at home variables (ASBG04) has the following valid values:

None or very few (0-10 books)
Enough to fill one shelf (11-25 books)
Enough to fill one bookcase (26-100 books)
Enough to fill two bookcases (101-200 books)
Enough to fill three or more bookcases (more than 200)

Remove the variables from the list of Independent background continuous variables list and add the variable ASBG04 (number of books at home) in the list of Independent background categorical variables. You will see that the list will automatically show the number of categories for the variable, a drop-down list with the different coding schemes (dummy, deviation and simple, see column N cat.), and the drop-down list with the variable’s categories to choose from:

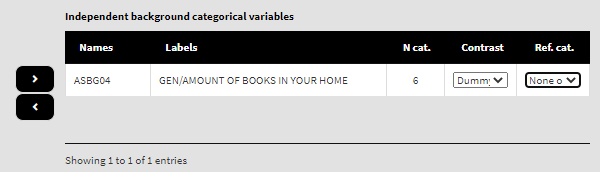
By default, dummy contrast coding scheme and the first available category as a reference are chosen. Let’s leave the defaults. The function will automatically compute the regression coefficients with dummy coding (the intercept will be the average overall reading achievement for students who have chosen the category we set as a reference, see further) and the regression coefficients for the rest of the categories will be the differences in achievement for the students who chose any other category, but the reference. If any other contrast scheme is needed, it can be changed by clicking on the drop-down menu and selecting either deviation or simple (for description of the different contrast coding schemes see here). We will leave the first category (“None or very few (0-10 books)” at home) as the reference. We will add how much students like reading scale (ASBGSLR, check the PIRLS 2016 technical documentation on how this scale is constructed and its properties) as a control variable in the list of Independent background continuous variables. We will leave the set of five PVs on overall reading achievement in the list of Dependent plausible values:

Because we use the application with Linear regression directly after performing the previous analysis, we still have the rest of the settings from the previous analysis done. There is no need to change any of the remaining settings, unless you want to. You could, though, change the output file name, otherwise it will be overwritten. Note that the displayed syntax will change, reflecting the removal of the variables from the previous analysis, and inclusion of the ASBG04 as independent categorical variable and ASBGSLR as independent background continuous variable:

Press the Execute syntax button. The GUI console will update, logging all completed operations:

If the Open the output when done checkbox is ticked, the output will open automatically in the default spreadsheet program (usually MS Excel) when all computations are completed. As with the previous analyses, refer to the explanations on the structure of the workbook, its sheets and the columns here.

RALSA – the R Analyzer for Large-Scale Assessments

This website provides resources on how to use the R Analyzer for Large-Scale Assessments (RALSA) to conduct analyses

Linear regression

Table of contents

Introduction

The linear regression function and its arguments

Computing linear regression coefficients using the command line

Computing linear regression coefficients using the GUI